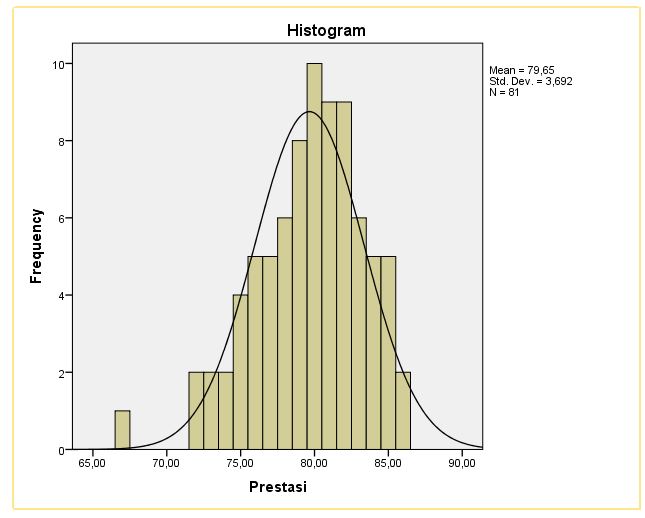
Data tidak normal dapat terjadi dalam analisis statistik ketika data tidak mengikuti distribusi normal atau distribusi Gaussian. Distribusi normal adalah distribusi yang simetris, di mana nilai rata-rata, median, dan modus berada pada titik yang sama. Data yang tidak normal dapat memiliki pola-pola yang berbeda seperti skewed (miring ke kiri atau kanan), bimodal (memiliki dua puncak), atau outliner (nilai-nilai terpencil yang sangat jauh dari nilai-nilai lainnya).
Ada beberapa alasan mengapa data tidak normal:
-
Sifat Alami Data: Kadang-kadang, sifat alami dari data itu sendiri menyebabkan data tidak normal. Misalnya, data keuangan seperti pendapatan atau harga saham cenderung tidak normal karena dapat memiliki skewness positif yang menyebabkan ekor yang panjang di sebelah kanan distribusi.
-
Error atau Gangguan: Kesalahan pengukuran atau adanya gangguan dapat mempengaruhi bentuk distribusi data. Contohnya, dalam survey atau eksperimen, sejumlah error dapat terjadi dalam mengumpulkan data sehingga menghasilkan distribusi yang tidak normal.
-
Data Outliner: Data outliner adalah nilai yang sangat jauh dari nilai-nilai lainnya dalam kumpulan data. Data outliner dapat mempengaruhi distribusi data, terutama jika jumlah data outliner tersebut signifikan.
-
Sampling Error: Sampling error dapat terjadi saat kita hanya memiliki sampel yang terbatas dari suatu populasi. Jika sampel tersebut tidak mewakili populasi dengan benar, maka distribusi data yang diperoleh tidak akan normal.
-
Transformasi Variabel: Beberapa analisis statistik memerlukan transformasi data untuk memenuhi asumsi distribusi normal. Misalnya, beberapa analisis membutuhkan transformasi logaritmik atau akar kuadrat dari variabel untuk menghasilkan distribusi yang lebih mendekati normal.
-
Distribusi Non-Parametrik: Kadang-kadang, kita tidak memiliki informasi tentang distribusi populasi yang sebenarnya. Dalam kasus tersebut, analisis statistik non-parametrik yang tidak memerlukan asumsi distribusi normal dapat digunakan.
Ketika kita menemui data yang tidak normal, penting untuk mempertimbangkan faktor apa yang menyebabkan ketidaknormalan tersebut dan bagaimana hal itu dapat mempengaruhi analisis statistik yang akan dilakukan. Dalam beberapa kasus, kita dapat mengubah variabel atau melakukan transformasi data untuk menghasilkan distribusi yang lebih normal. Namun, dalam kasus lain, analisis statistik non-parametrik atau metode lain yang robust terhadap ketidaknormalan mungkin lebih sesuai.
Dalam rangka menginterpretasikan hasil analisis statistik dengan data yang tidak normal, kita juga perlu secara hati-hati memeriksa asumsi dan penggunaan metode yang tepat untuk menghindari kesalahan interpretasi dan kesimpulan yang keliru.